含水层非均质性的表征方法

网疯

水文地质参数是确定地下水模型的基础和关键，这一阶段就是通常所说的地下水逆问题，也称水文地质参数反演。水文地质参数包括渗透系数、给水度、贮水率等，其中渗透系数最为重要。
考虑到非均质渗透系数场的反演估计通常会导致的高维问题，高维参数受制于维数灾难问题。渗透系数场的维度取决于网格剖分程度，后面的数值算例的维度为（51 \times 71=3621），为了在可接受的计算时间内解决高维参数反演问题，通常需要对渗透系数场进行表征（概化和降维）。这篇文章介绍常用的非均质表征方法。
为了方便后续的方法介绍，先简单设计地下水模拟算例：
考虑非均质各向同性承压含水层，含水层水流运动为稳定流。研究区大小为 12.5 [L]×17.5 [L]，离散为 51×71的均匀网格（网格尺寸为 0.25 [L] ×0.25 [L]）。含水层厚度为 1 [L]。南北边界为二类隔水边界，东西边界为定水头边界，水头分别为 6 [L]和 5 [L]。
分区法（zonation method）

实际工程中应用最常用的含水层非均质性表征方法——分区法：通过水文地质调查根据场地的水文地质条件进行水文地质参数分区，假定各分区内的含水层均质（即：每个子区域内水文地质参数为固定值），分区之间含水层非均质。
假设将含水层分为3个参数分区（zone-1，zone-2，zone-3）

Zone id	K value （m/d）
Zone-1	4.5
Zone-2	15.5
Zone-3	10.0

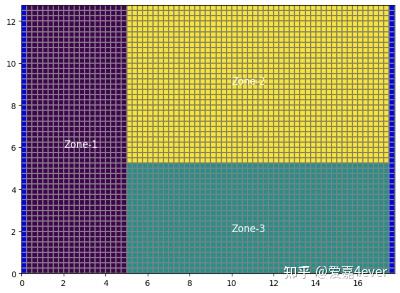
图1 分区法示意图

分区法的模型实现相对简单，因此在场地模型和矿山水文地质等领域仍是主要的方法之一。当研究区不大且分区数目足够的情形下，分区法能够在一定程度上刻画出渗透系数的非均质性。但是，分区法对建模者的地质和水文地质要求较高，分区具有较大的主观性。
向导点法（pilot point method）

向导点法是利用向导点处的渗透系数值进行插值运算，从而得到整个场地的渗透系数场。
假定存在12个向导点，这里可以练习下利用表格所列的向导点数据（x, y, K_value)得到渗透系数场[1]

pp id	row	column	X坐标	Y坐标	K_value
1	3	5	1.125	12.125	8.81
2	3	25	6.125	12.125	5.89
3	3	45	11.125	12.125	5.23
4	3	65	16.125	12.125	4.25
5	23	5	1.125	7.125	10.36
6	23	25	6.125	7.125	8.94
7	23	45	11.125	7.125	6.83
8	23	65	16.125	7.125	5.16
9	43	5	1.125	2.125	2.59
10	43	25	6.125	2.125	9.22
11	43	45	11.125	2.125	3.88
12	43	65	16.125	2.125	7.24

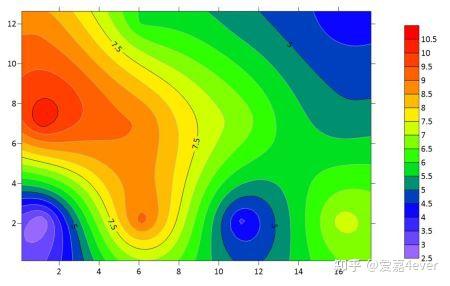
图2 利用指数型变差函数得到的渗透系数场

在地下水正问题中，就是选择适合的插值算法（比如kriging方法）得到如图2的渗透系数场，该渗透系数场作为地下水模型的输入参数。图3是利用flopy得到的渗透系数场以及向导点示意图。



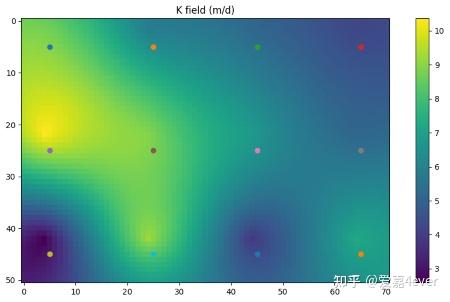
图3 渗透系数场及向导点示意图

向导点法通常需要结合地质统计类方法进行，对于确定性模型需要连接Kriging等插值方法，对于随机地下水模型则需要结合地质统计随机建模方法（比如Sgsim等方法）。
需要说明的是，上述利用向导点方法计算变差函数和利用Kriging插值的过程中，未考虑渗透系数场通常是满足对数正态分布的特点，这是不合适的。正确的方法是对K_value列进行处理，得到 ln(K_{value})，然后进行处理。
相较于分区法，向导点法考虑了空间相关性，渗透系数场更为合理，具有空间连续性、可迁性等特点，但是模型实现较为困难，需要建模者兼具地下水数值模拟和地质统计学模拟的相关知识。
Karhunen-Loѐve展开方法

假设渗透系数场服从对数正态分布，且满足二阶平稳假设（这个条件通常是满足的） ，其变差函数为：
\gamma_{lnK}=\sigma^2_{lnK}exp(\sqrt{(\frac{x_1-x_2}{\lambda_x})^2+(\frac{y_1-y_2}{\lambda_y})^2})
其中， （x_1,y_1） 和 （x_2,y_2） 是任意两个位置， \lambda_x 和 \lambda_y 是相关长度。假定含水层 lnK 均值为2.0，方差为0.5，\lambda_x 和 \lambda_y 分别为6[L]和3[L]。
这里，我们运用一种主成分分析方法（Karhunen-Loѐve展开方法，KLE方法）参数化对数渗透系数场[2]， lnK 可表示为：
lnK(x,y)\approx ln\bar{K}(x,y)+\sum_{i=1}^{N_{KL}}{\xi_i\sqrt{\tau_i}}s_i(x,y)
其中， ln\bar{K}(x,y) 是对数渗透系数场的均值， \xi_i 是独立的标准高斯正态分布变量， \tau_i 和 s_i 分别是特征值和特征函数。 N_{KL} 为KLE方法的展开项数，项数越大，能够保留更多的渗透系数场的不确定性。对于本算例而言， N_{KL}=200 时能保留渗透系数场 96.7% 的非均质性特征。



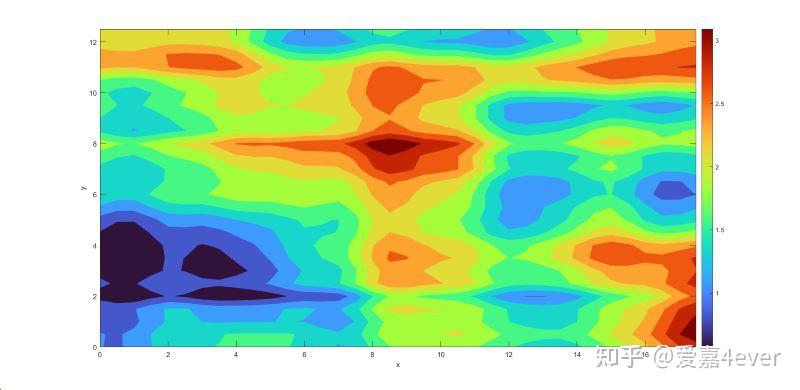
图4 利用KLE展开生成的渗透系数场

% Karhunen-Loѐve
clear all;clc
% Size of domain
Lx = 17.5;
Ly = 12.5;
% Discretization
dx = 0.5;
dy = 0.5;
n = Ly/dy+1;   % row number
m = Lx/dx+1;   % column number
% Correlation lengths
lambdax = 6;
lambday = 3;
% Field mean and variance
MeanY = 2.0;
VarY = 0.5;
% Correlation function
C = nan(m*n,m*n);
x = nan(m*n,2);

for i =1:m*n  
    a=rem(i,m);
    b=fix(i/m);
    if(a==0)
        x(i,1)=(m-1)*dx;
        x(i,2)=(b-1)*dy;
    else
        x(i,1)=(a-1)*dx;
        x(i,2)=b*dy;
    end
end

for i = 1:m*n
    for j = 1:m*n
        C(i,j) = VarY*exp(-(abs((x(i,1)-x(j,1))/lambdax)+abs((x(i,2)-x(j,2))/lambday)));
    end
end
% Calculate eigenvalues and eigenvectors
kl_num = 200;          % number of KL terms that are preserved
[A1,B1] = eigs(C,kl_num); % returns the k largest magnitude eigenvalues.
rng(1001,'twister') % 保证每次以seed=1001的情形下的随机数是相同的，便于模型复现
kl_term = randn(kl_num,1);
Y = MeanY + A1*sqrt(B1)*kl_term;
ratio = cumsum(diag(B1)) / (m * n * VarY);
kle_percentage = ratio(end);
figure
contourf(0:dx:Lx,0:dy:Ly,reshape(Y,m,n)',10,'linestyle','none')
xlabel('x');
ylabel('y');上面介绍的是几种常用的渗透系数场降维方法。近些年基于深度学习的降维方法逐步涌现（比如VAE, CVAE, GAN等等），感兴趣的可以自行搜索。
参考

• ^利用地质统计学方法刻画渗透系数 https://zhuanlan.zhihu.com/p/563466616
  
• ^地下水污染源解析的贝叶斯监测设计与参数反演方法 http://cdmd.cnki.com.cn/article/cdmd-10335-1017071503.htm